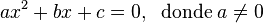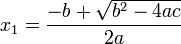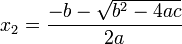PASOS PARA RESOLVER UNA ECUACION CUADRATICA: 2016

ECUACION BICUADRADA

Éstas son un caso particular de la ecuación de cuarto grado. Les faltan los términos a la tercera y a la primera potencia. Su forma polinómica es:

ax^4 + {bx^2}^{} + c = 0

Para resolver estas ecuaciones tan solo hay que hacer el cambio de variable

{x^2}^{}=u

Con lo que nos queda:

{au^2}^{} + bu + c = 0

El resultado resulta ser una ecuación de segundo grado que podemos resolver usando la fórmula:

u_1 = \frac{-b + \sqrt{b^2-4ac}}{2a}, \qquad u_2 = \frac{-b - \sqrt{b^2-4ac}}{2a}

Al deshacer el cambio de variable aparecen las cuatro soluciones:

x_1 = +\sqrt{u_1}

x_2 = -\sqrt{u_1}

x_3 = +\sqrt{u_2}

x_4 = -\sqrt{u_2}

Ecuación bicuadrada simétrica

Que asume la forma

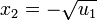
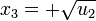
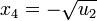
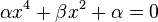
$\alpha x^4 + \beta x^2 + \alpha = 0$

Sin término independiente

Son de la forma:

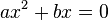$ax^2+ bx = 0$ , cuyas raíces son $x_1 = 0; x_2 = \frac{-b}{a}$

Sin término lineal

Son de la forma

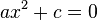ax^2+ c = 0

, cuyas raíces son reales opuestos o imaginarios puros opuestos.

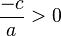Si $\frac {-c}{a} > 0$ las raíces son reales: $x_1= \sqrt {\frac {-c}{a}}$ o $x_2 = -\sqrt {\frac {-c}{a}}$

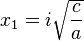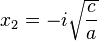
Si $\frac {-c}{a} < 0$ las raíces son imaginarias puras: $x_1= i\sqrt {\frac {c}{a}}$ o $x_2 = -i\sqrt {\frac {c}{a}}$

Solo el término de segundo grado

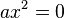$ax^2 = 0$ cuya raíz doble es igual a 0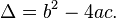

En la fórmula anterior, la expresión dentro de la raíz cuadrada recibe el nombre de discriminante de la ecuación cuadrática. Suele representarse con la letra D o bien con la letra griega Δ (delta) en mayúscula:

\Delta = b^2 - 4ac.\,

Una ecuación cuadrática con coeficientes reales tiene o bien dos soluciones reales distintas o una sola solución real demultiplicidad 2, o bien dos raíces complejas. El discriminante determina la índole y la cantidad de raíces.

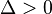Si $\Delta > 0$ hay dos soluciones reales y diferentes (la parábola cruza dos veces el eje de las abscisas: X):

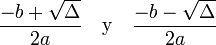\frac{-b + \sqrt {\Delta}}{2a} \quad\text{y}\quad \frac{-b - \sqrt {\Delta}}{2a}

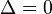Si $\Delta = 0$ hay una solución real doble (la parábola sólo toca en un punto al eje de las abscisas: X):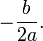

-\frac{b}{2a} . \,\!

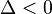Si $\Delta < 0$ hay dos soluciones complejas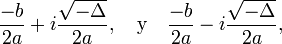 conjugadas (la parábola no corta al eje de las abscisas: X):

\frac{-b}{2a} + i \frac{\sqrt {-\Delta}}{2a}, \quad\text{y}\quad \frac{-b}{2a} - i \frac{\sqrt {-\Delta}}{2a},

donde i es la unidad imaginaria.

HISTORIA DE LA ECUACION CUADRATICA

El origen y la solución de las ecuaciones de segundo grado es muy antiguo. En Babilonia se conocieron algoritmos para resolverla. Fue encontrado independientemente en otros lugares del mundo. En Grecia, el matemático Diofanto de Alejandría aportó un procedimiento para resolver este tipo de ecuaciones (aunque su método sólo proporcionaba una de las soluciones, incluso en el caso de que las dos soluciones sean positivas). La primera solución completa la desarrolló el matemático Al-Juarismi (o Al-Khwarizmi según otras grafías), en el siglo IX en su trabajo Compendio de cálculo por reintegración y comparación, cerrando con ello un problema que se había perseguido durante siglos. Basándose en el trabajo de Al-Juarismi, el matemático judeoespañol Abraham bar Hiyya, en su Liber embadorum, discute la solución de estas ecuaciones. Hay que esperar a Évariste Galois para conseguir resolver en general las ecuaciones polinómicas, o saber cuándo son irresolubles por radicales, que viene a ser una generalización de los métodos de resolución de las ecuaciones de segundo grado.

La primera gran dificultad pudo surgir en la solución de ecuaciones cuadráticas se dio con la ecuación

x^2 - 2 = 0

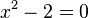en la época de los pitagóricos, al calcular la longitud de la diagonal de un cuadrado de lado 1 ya que no se podía expresar la raíz cuadrada de dos como razón de dos números enteros. .

En el Renacimiento al resolver

x^2 + 1 = 0

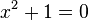que requiere hallar un número real cuyo cuadrado sea -1, se superó con la adopción de números imaginarios y la definición de la unidad imaginaria i que cumple

i^2 = -1

PASOS PARA RESOLVER UNA ECUACION CUADRATICA

Primero que nada: ¿Que es una ecuación cuadrática?

es una ecuación que tiene la forma de una suma algebraica de términos cuyo grado máximo es dos, es decir, una ecuación cuadrática puede ser representada por un polinomio de segundo grado o polinomio cuadrático. La expresión canónica general de una ecuación cuadrática de una variable es:

$ax^2 + bx + c = 0,\;\;\mbox{donde}\;a\neq 0$

MÉTODO FORMULA GENERAL.

La formula general que se utiliza para encontrar las raizes de una ecuación cuadrática resulta (se despeja la incógnita) de la expresión canónica general anterior.

Despejando la incógnita x de la forma general se obtiene la formula general:

$x = \frac{-b \pm \sqrt {b^2-4ac}}{2a}$

Se usa ± para indicar las dos soluciones:

x_1 = \frac{-b + \sqrt {b^2-4ac}}{2a}

\ x_2 = \frac{-b - \sqrt {b^2-4ac}}{2a}

PASOS PARA RESOLVER UNA ECUACIÓN CUADRÁTICA

CON FORMULA GENERAL.

Verificar que la ecuación esta igualada en su forma canónica (si no lo esta, igualarla a cero).
Identificar los valores de a,b y c.
Sustituir los valores de a,b y c en la formula general.
Resolver la ecuación utilizando el orden jerárquico de las operaciones.
Se llega al calculo de las raizes.

PASOS PARA RESOLVER UNA ECUACION CUADRATICA

miércoles, 27 de enero de 2016

ECUACION BICUADRADA

Ecuación bicuadrada simétrica

ECUACIONES INCOMPLETAS

Sin término independiente

Sin término lineal

Solo el término de segundo grado

DISCRIMINANTE

HISTORIA DE LA ECUACION CUADRATICA

PASOS PARA RESOLVER UNA ECUACION CUADRATICA